domicmeia/[Multicoreprogramming]DP

공부 목적으로 작성한 포스팅입니다. 오타가 많고, 틀린 내용이 있을 수 있습니다.

목차

1. 재귀 - 피보나치
2. DP 사용 조건
3. 분할 정복 vs 동적 계획법
4. DP 모델화
5. DP 적용 방법

일단 동적 계획법(Dynamic Programming)은 큰 문제를 작은 문제로 나눠서 푸는 알고리즘이다. 피보나치 수열을 예로 들자.

재귀 - 피보나치

int fibo(int n)
  {
    if (n<=2)
      return 1;
    else
      return fibo(n-1) + fibo(n-2);
   }

이 함수는 피보나치 수열의 n번째 수를 구하는 함수이다. fibo(6)은 아래와 같이 진행된다. 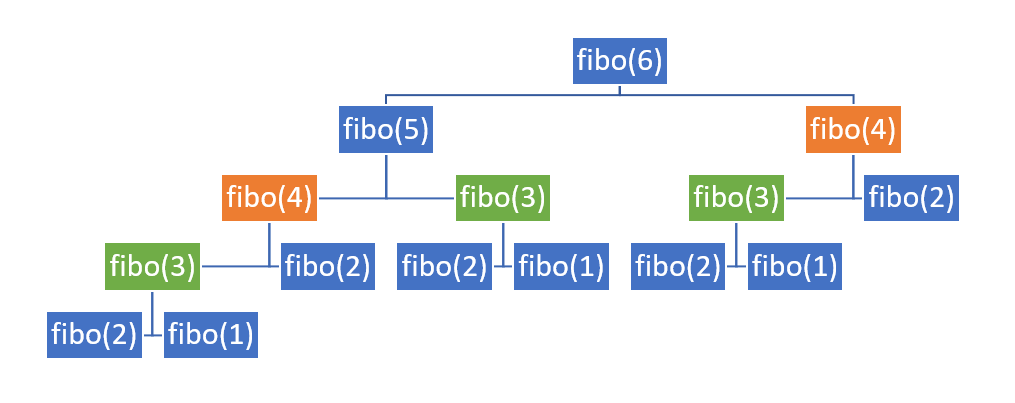이미 진행된 연산인 fibo(4)와 fibo(3)이 여러번 진행된 것을 볼 수 있다. 이러한 반복 연산의 결점을 보완한 알고리즘이 바로 DP이다.

DP 사용 조건

DP가 적용되기 위해서는 2가지 조건을 만족해야 한다. Optimal Substructure와 Overlaping SubProblem이다. 계속 예를 들어보자. 피보니치 수열의 식은 F(n)=F(n-1)+F(n-2) (n>2)이다. 이 식은 다음의 두 가지를 보인다.

1. F(n-1)과 F(n-2)을 더하면 F(n)이 나온다.
2. 귀납법의 증명을 통해 n=k일 때 성립하면 n=k+1도 성립한다. 즉, F(k+1)=F(k)+F(k-1)또한 성립한다.

첫번째를 Optimal Substructure(최적 부분 구조)라 한다. 큰 문제의 정답을 작은 문제를 통해 풀이하는 것을 의미한다. 그래서 특정 문제의 정답은 문제의 크기에 상관없이 항상 동일하다. 예를 들어 A 지점에서 B지점까지 가는 중간에 X가 있다고 가정하자. A에서 X로 가는 경우의 수가 얼마나 많든, X에서 B로 가는 경우의 수가 얼마나 많든 상관없이 A-X/X-B가 가장 짧은 경로라면 전체 최적 경로도 A-X-B이다. 이와 같이 부분 문제에서 구한 최적 결과가 전체 문제에서 동일하게 적용되어 결과가 변하지 않을 때 DP를 사용할 수 있다.

두번째를 Overlaping SubProblem(중복 부분 문제)라 한다. 예를 들어 F(4)=F(3)+F(2)과 F(3)=F(2)+F(1) 식에서 F(3)과 F(2)항이 겹친다. DP는 기본적으로 문제를 나누고 그 문제의 결과값을 재활용하여 전체 답을 구한다. 그래서 동일한 작은 문제들이 반복하여 나타나는 경우에만 사용이 가능하다. 그러므로 우리는 1회 계산했을 때의 값을 저장해 다음 피보나치 식에서 이를 재사용한다.

분할 정복 vs 동적 계획법

분할 정복

• 연관 없는 부분문제로 분할 한다.
• 부분문제를 독립, 재귀적으로 해결한다.
• 부분문제의 해를 결합한다.
• 하향식 방법으로 접근

DP

• 모든 부분문제는 연관되어 있다.
• 모든 부분문제를 한번만 계산하고 결과를 저장하고 재사용한다.
• 분할 정복은 같은 부분문제가 나타날 경우 다시 계산한다.
• 보통 상향식 방법으로 접근 but 하향식 방법으로도 구현 가능(e.g. TSP 문제 - 반복 재귀DP)

DP 모델화

동적 계획법은 큰 문제를 이루는 작은 문제들을 먼저 해결하고 작은 문제들의 최적 해를 이용하여 순환적으로 큰 문제를 해결한다. 또한 DP는 문제의 순환적인 성질 때문에 이전에 계산되어졌던 작은 문제의 해가 다른 어딘가에서 필요하게 되는데, 이를 위해 이미 해결된 문제들의 해들을 어떤 저장 공간에 저장하게 된다. 그리고 이렇게 저장된 해들이 다시 필요할 때 마다 해를 얻기 위해 다시 문제를 재계산하지 않고 table의 참조를 통해서 중복된 계산을 피하게 된다. 따라서 DP는 DAG(사이클이 없는 유형)으로 모델화된다. 그래프를 다루는 요소는

• 정점 : 문제에서의 특정 상황을 유일하기 결정짓는 변수들로 이루어진 상태
• 간선 : 상태간의 전이를 나타내는 점화식

각 정점은 현재 상태에 대한 답을 갖고, 이러한 답을 나타내는 배열을 dp라고 이름을 짓는다. 예를 들어 변수가 x, y라면 dp[x][y] 같은 형태로 상태의 답을 나타낸다. 우리는 최소한의 상태와 최소한의 점화식을 사용하여 전체 상황을 표현할 수 있어야 한다. 문제로 연습해보자. 이 문제에서의 상태는

• dp[x]: x를 1로 만들기 위해 필요한 최소의 연산 횟수

그럼 각 상태를 결정하기 위해 어떤 점화식을 세울 수 있을까. 다음과 같이 생각해 볼 수 있다.
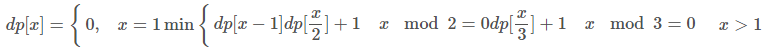
혹시나 순서대로 3으로 나눌 수 있을 때 3으로 나누고, 2로 나눌 수 있을 때 2로 나누고 1을 빼면 되지 않을까라는 생각은 버려야 한다. 10의 경우, 10-5-4-2-1 보다 10-9-3-1이 연산횟수가 적다. 따라서 이 문제는 DP로 풀어야 한다.

DP 적용 방법

1. Top-Down
2. Bottom-Up

Top-Down은 간단히 말해 재귀 함수를 사용하는 방법이다. 가장 큰 문제를 방문 후 작은 문제를 호출한다. 점화식을 이해하기 쉽다는 장점이 있다. 이 방식(Memozation¹)은 하향식이라고도 한다. 피보나치 수열을 다시 생각해 보자. 피보나치 수을 구하는 알고리즘에서 fibo(n)의 값을 계산하자마자 저장하면, 실행시간을 O(n)으로 줄일 수 있다.

//memo를 위한 배열을 할당하고, 모두 -1으로 초기화 한다.
//memo[0]을 0으로 memo[1]는 1로 초기화 한다.

fibo(n)
     IF n > 2 AND memo[n] = -1
            memo[n] <- fibo(n-2) + fibo(n-2)
     Return memo[n]

하지만 재귀 함수 호출로 인한 시스템 호출 스택을 사용하게 되고 실행 속도 저하 또는 오버플로우가 발생할 수 있다. 이를 해결하기 위해서 반복문을 사용하는 방식도 있다. 이 방식(Tabulation)을 Bottom-Up이라하며, 상향식이라고도 불린다. 가장 작은 문제들부터 답을 구해가며 전체 문제의 답을 찾으며 시간과 메모리 사용량을 줄일 수 있다. 피보나치 수열을 이 방식으로 풀면

fibo(n)
     fibo[0] <- 0
     fibo[1] <- 1
     FOR i in 2 -> n
            fibo[i] <- fibo[i-1]+fibo[i-2]
     Return fibo[n]

그럼 위의 문제를 두 가지 방법으로 구현해보자.

Top-Down

#include <iostream>
#include <algorithm>
using namespace std;

int db[1000002];

int go(int n) {
	if (n == 1) return 1;
	if (db[n] > 0) return db[n];
	int ret = go(n - 1) + 1;
	int temp;

	if (n % 3 == 0) {
		temp = go(n / 3) + 1;
		if (ret > temp) ret = temp;
	}

	if (n % 2 == 0) {
		temp = go(n / 2) + 1;
		if (ret > temp) ret = temp;
	}
	db[n] = ret;
	return ret;

}
int main(void) {
	int x;
	int cnt=0;
	cin >> x;
	
	cout << go(x)-1;
	return 0;
}

Bottom-Up

#include <iostream>
#include <algorithm>
using namespace std;

int db[1000002];

int main(void) {
	int x;
	db[1] = 0;
	cin >> x;
	
	for (int i = 2; i <= x; ++i) {
		db[i] = db[i-1] + 1;
		if (i % 2 == 0)
			db[i] = min(db[i], db[i / 2] + 1);
		if (i % 3 == 0)
			db[i] = min(db[i], db[i / 3] + 1);
	}
	cout << db[x];

	return 0;
}